from pandas import TimedeltaIndex
from weldx import Q_, MathematicalExpression, TimeSeries
from weldx.measurement import (
Error,
MeasurementChain,
MeasurementEquipment,
Signal,
SignalSource,
SignalTransformation,
)
8. MeasurementChain Tutorial#
8.1. Overview#
The goal of the MeasurementChain class is to describe as detailed as possible how experimental data is acquired.
Acquiring this data is a process that usually involves multiple substeps. For example, during a temperature measurement we might have a sensor that produces a voltage correlating with the current temperature.
Since we wanted to know the temperature and not some arbitrary voltage, we need to transform the voltage data into temperature data by utilizing the calibration of our sensor.
The MeasurementChain is build upon 2 basic constructs: Signals and transformations.
We always start our measurement chain with an initial signal, generated by a source sensor.
In the example we gave before this was a voltage.
To get to the data of interest we might need to perform one or more transformation steps were each one yields a new signal.
Possible transformations are for example an AD conversion, signal amplification, filtering, or applying a calibration.
The last signal of the measurement chain is usually the one we generate our measurement data from by recording its value at certain points in time.
We will now discuss the different methods to construct a MeasurementChain and the features it offers.
8.2. Construction without additional classes#
The easiest way to construct a measurement chain is to use the from_parameters and the create_transformation methods. With these functions, we do not need to bother with as many extra classes as with the other approaches.
We start with the from_parameters function to create a new measurement chain. We need to provide 5 parameters to it:
The name of the measurement chain
The name of the source that creates the first, unprocessed measurement signal
The error of the source
The type of the source signal (analog or digital)
The unit of the source signal
Optionally, one can also provide the associated measurement data, if it was recorded, but we will discuss this in a later section. Let’s start by creation our first measurement chain:
mc_1 = MeasurementChain.from_parameters(
name="Temperature measurement chain 1",
source_name="Thermocouple 1",
source_error=Error(deviation=Q_(0.1, "percent")),
output_signal_type="analog",
output_signal_unit="V",
)
As you can see, we have created a MeasurementChain with the name “Temperature measurement chain 1”. It’s source is named “Thermocouple 1” and it produces an analog output signal in Volts. The specified measurement error is a fixed value of 0.1%.
Next we want to add the first transformation step, the analog-digital conversion of the signal. Therefore, we use the create_transformation method of our newly created measurement chain. As the from_parameters function, it accepts the name of the transformation, its error, the output signal, and the output unit as parameters. Additionally, we can provide a function that describes how the numerical values and units are transformed.
The output signal type, unit and function are all optional parameters. However, providing none of them wouldn’t apply any changes to the signal and emit a warning.
Now we add the AD conversion to our measurement chain:
mc_1.create_transformation(
name="AD conversion",
error=None,
output_signal_type="digital",
output_signal_unit="",
)
All we needed to specify apart from the name and error was the output signal type as “digital”. We also removed the unit by providing an empty string as output unit since the AD conversion just yields a digital number that doesn’t necessarily represent a physical quantity.
Let’s add the final transformation, the calibration, which produces the data we are interested in.
mc_1.create_transformation(
name="Calibration",
error=Error(Q_(0.4, "percent")),
func=MathematicalExpression(
expression="a*x+b", parameters={"a": Q_(3, "K"), "b": Q_(273.15, "K")}
),
)
Here we specify a function that describes the transformation of our digital number into an actual temperature value:
$$ 3K \cdot x + 273.15K $$
The name of the variable and the parameters can be arbitrarily chosen. The only restriction is, that the function only has a single variable which represents the input signal. In this example our input variable is given by x.
Since the parameters of our function already contain the unit conversion we do not need to provide the output_signal_unit parameter.
However, we could do this to assure that the functions’ output signal has the correct dimensionality, for example length, time, or temperature.
To do so, we can provide an arbitrary unit of the desired dimension.
If we would pass m, we expect the output signal to represent a length.
In case the function yields inches, millimeters, yards etc. this would be the correct dimensionality.
Squaremeters, seconds, or volts would raise an exception.
Additionally, you can’t use the output_signal_unit parameter to add a unit conversion if the passed function does not contain one. In fact, if only output_signal_unit is provided without a function, like in the AD conversion we added before, create_transformation generates a corresponding conversion function internally.
8.3. Plotting measurement chains#
Now that we have created our first measurement chain without any exceptions, we might want to verify that everything is specified correctly. To do so, we can use pythons print command to check all variables, but this would be a bit tedious. A more convenient way is to use the plot function of the MeasurementChain.
mc_1.plot()
<Axes: title={'center': 'Temperature measurement chain 1'}>
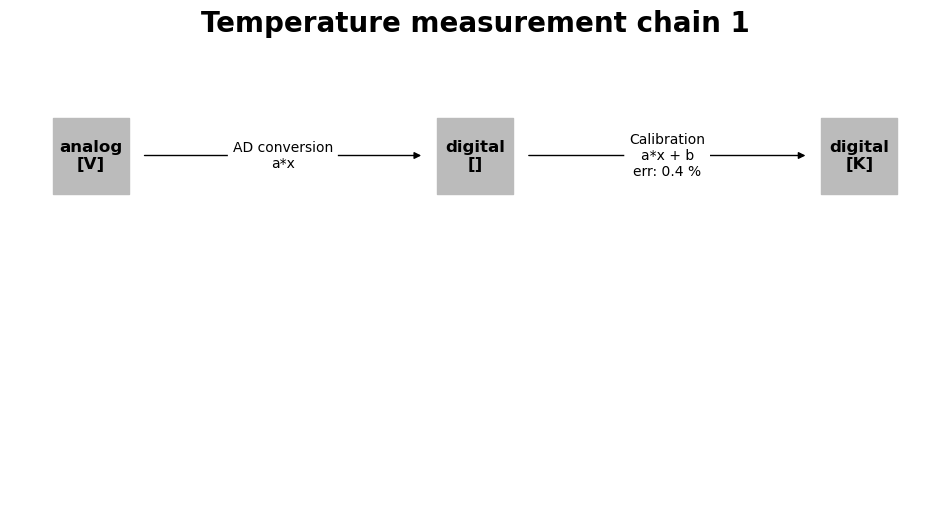
The plot shows us the initial signal produced by the source on the left. To the right of the source signal all transformations and their resulting output signals are shown.
8.4. Construction from dedicated classes#
The first method we demonstrated required you to provide a lot of parameters. While this method is very explicit and doesn’t involve many other classes, it is not the best approach if you want to share sources and transformations with other measurement chains or objects. To share information about a source or transformation, two dedicated container classes are available: SignalSource and SignalTransformation.
A SignalSource can be generated as follows:
source_2 = SignalSource(
name="Source",
error=Error(Q_(0.1, "percent")),
output_signal=Signal(signal_type="analog", units="V"),
)
The information we provide is similar as before. The only noteworthy thing here is, that the signal type and unit are wrapped into a separate Signal class. Now we can use this class to create a measurement chain:
mc_2 = MeasurementChain(name="Measurement chain 2", source=source_2)
mc_2.plot()
<Axes: title={'center': 'Measurement chain 2'}>

Next we create a SignalTransformation
transformation_3 = SignalTransformation(
name="Transformation",
error=Error(Q_(1, "percent")),
func=MathematicalExpression(
expression="a*x+b", parameters={"a": Q_(3, "K/V"), "b": Q_(273.15, "K")}
),
type_transformation="AD",
)
The first three arguments are equivalent as when using the create_transformation method. The type_transformation parameter expects a string consisting of two letters that can either be “A” for analog and “D” for digital. The first letter is the expected input signal type and the second letter the output signal type.
We can add it to the MeasurementChain with the add_transformation function.
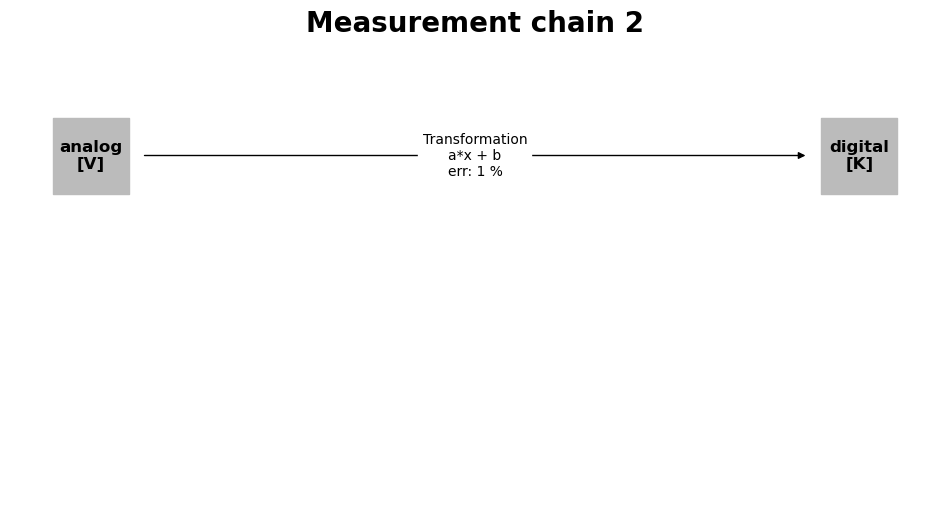
mc_2.add_transformation(transformation_3)
mc_2.plot()
<Axes: title={'center': 'Measurement chain 2'}>
8.5. Construction from equipment classes#
The sources and transformations of a measurement chain are often tied to a certain piece of laboratory equipment.
The weldx package offers the MeasurementEquipment structure to describe your equipment and collect all the operations it performs inside of a measurement chain.
Since lab equipment usually doesn’t change frequently, a good approach would be to define all your instruments once and reuse their definitions when creating a new WelDX file.
The MeasurementChain supports this by letting you create a new instances using from_equipment and adding transformations with add_transformation_from_equipment.
Let us create two pieces of equipment and create a new MeasurementChain from it:
source_eq = MeasurementEquipment("Source 2000", sources=[source_2])
transformation_eq = MeasurementEquipment(
"Transformer X3", transformations=[transformation_3]
)
Now we simply create a measurement chain from them:
mc_3 = MeasurementChain.from_equipment("Measurement Chain 3", source_eq)
mc_3.plot()
<Axes: title={'center': 'Measurement Chain 3'}>

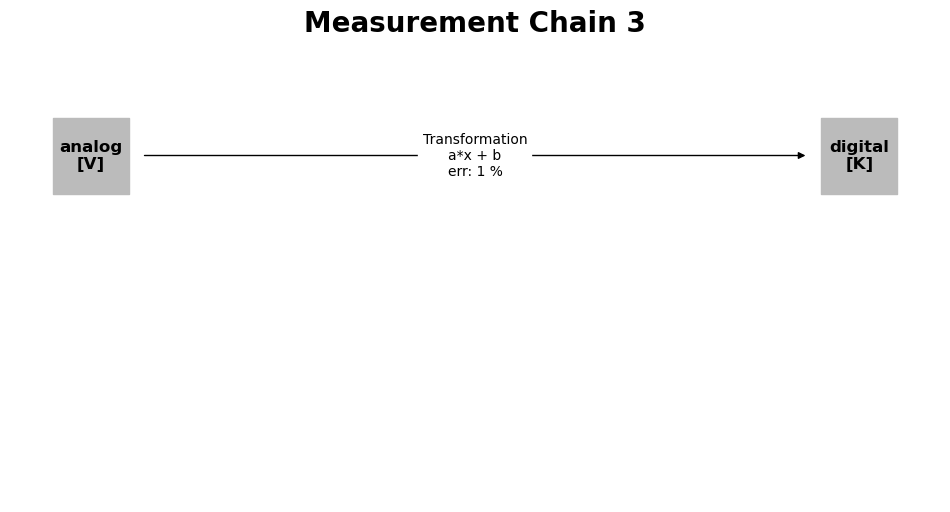
mc_3.add_transformation_from_equipment(transformation_eq)
mc_3.plot()
<Axes: title={'center': 'Measurement Chain 3'}>
If we add an equipment to the MeasurementChain, it won’t just only store the corresponding transformation but also remember the equipment that provides it.
We can get the linked equipment using get_equipment.
Therefore we must provide the name of the transformation or source
mc_3.get_equipment("Source")
MeasurementEquipment(name='Source 2000', sources=[SignalSource(name='Source', output_signal=Signal(signal_type='analog', units=<Unit('volt')>, data=None), error=Error(deviation=<Quantity(0.1, 'percent')>))], transformations=[])
It might also be the case that an equipment provides multiple sources or transformations.
In this case, you need to specify which one should be added to the MeasurementChain.
The from_equipment and add_transformation_from_equipment provide an extra parameter for this case.
8.6. Accessing information#
In case you want to know names of the source or the transformations that are part of a MeasurementChain, you can use the following two properties:
mc_3.source_name
'Source'
mc_3.transformation_names
['Transformation']
You can also get the the SignalSource and SignalTransformation objects using:
mc_3.source
SignalSource(name='Source', output_signal=Signal(signal_type='analog', units=<Unit('volt')>, data=None), error=Error(deviation=<Quantity(0.1, 'percent')>))
mc_3.get_transformation("Transformation")
SignalTransformation(name='Transformation', error=Error(deviation=<Quantity(1, 'percent')>), func=<MathematicalExpression>
Expression:
a*x + b
Parameters:
a = 3 K / V
b = 273.15 K
, type_transformation='AD', input_shape=None, output_shape=None, meta=None)
Because a measurement chain can contain multiple transformations, you have to specify the name of the desired transformation when using get_transformation.
If you want to know the type and unit of a signal that is generated by the source or results from a transformation, you can call the get_signal method.
It returns a special class that contains all relevant information about a signal, including attached measurement data, that will be covered in the next section.
mc_3.get_signal("Transformation")
Signal(signal_type='digital', units=<Unit('kelvin')>, data=None)
One can also get a list of all signals and transformations with:
mc_3.signals
[Signal(signal_type='analog', units=<Unit('volt')>, data=None),
Signal(signal_type='digital', units=<Unit('kelvin')>, data=None)]
mc_3.transformations
[SignalTransformation(name='Transformation', error=Error(deviation=<Quantity(1, 'percent')>), func=<MathematicalExpression>
Expression:
a*x + b
Parameters:
a = 3 K / V
b = 273.15 K
, type_transformation='AD', input_shape=None, output_shape=None, meta=None)]
8.7. Attaching data#
Until now we have seen how to create such a MeasurementChain and how we can access the information it provides.
However, the most important information is currently still missing: the actual data we produced.
Attaching data is simply done with add_signal_data:
mc_1.add_signal_data(
TimeSeries(data=Q_([10, 15, 5], "K"), time=TimedeltaIndex(data=[0, 2, 6], unit="s"))
)
/tmp/ipykernel_3350/2937572707.py:2: FutureWarning: The 'unit' keyword in TimedeltaIndex construction is deprecated and will be removed in a future version. Use pd.to_timedelta instead.
TimeSeries(data=Q_([10, 15, 5], "K"), time=TimedeltaIndex(data=[0, 2, 6], unit="s"))
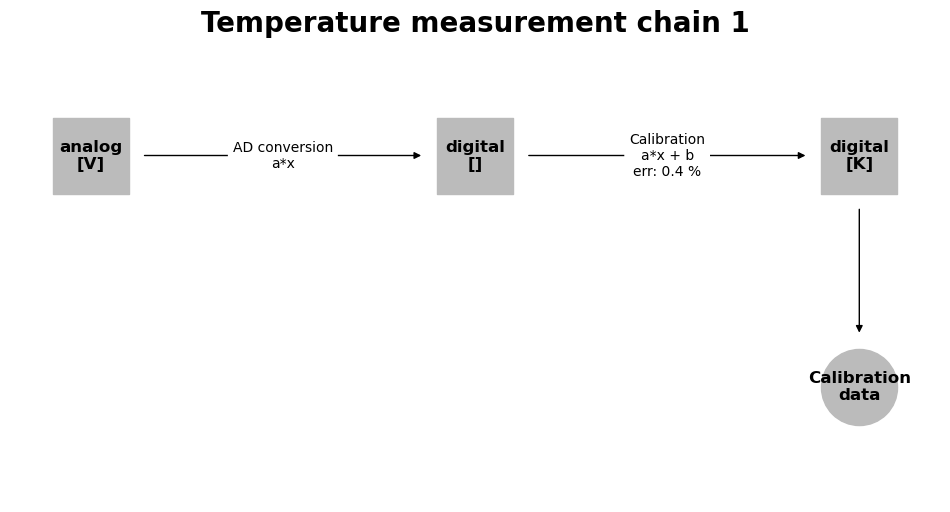
As you can see in the following plot, the data is associated with the output signal of the last transformation:
mc_1.plot()
<Axes: title={'center': 'Temperature measurement chain 1'}>
But what if we want to attach the raw data of our source too?
For this case, add_signal_data provides a second parameter to specify the origin of the data.
To add some data to the source, we do the following:
mc_1.add_signal_data(
data=TimeSeries(
data=Q_([2, 3, 1], "K"), time=TimedeltaIndex(data=[0, 2, 6], unit="s")
),
signal_source="Thermocouple 1",
)
/tmp/ipykernel_3350/1091637366.py:3: FutureWarning: The 'unit' keyword in TimedeltaIndex construction is deprecated and will be removed in a future version. Use pd.to_timedelta instead.
data=Q_([2, 3, 1], "K"), time=TimedeltaIndex(data=[0, 2, 6], unit="s")
As can be seen in the next plot, we successfully added the data to the source:
mc_1.plot()
<Axes: title={'center': 'Temperature measurement chain 1'}>
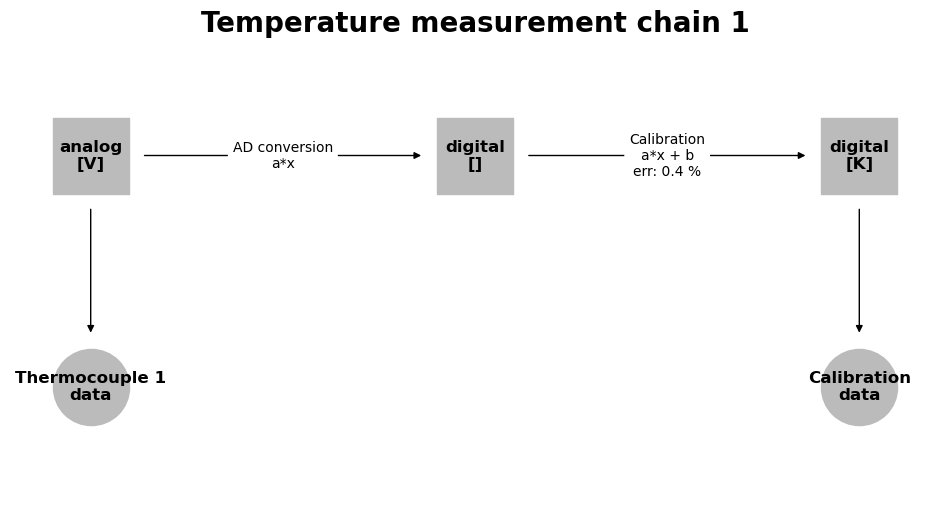
Also note, that all functions that let you create a measurement chain or add a transformation provide an extra parameter to add the corresponding data.
Finally, if you want to access the stored data, we can use get_signal_data.
As for the add_signal_data function, you get the data from the last transformation if you don’t specify any source or transformation name:
mc_1.get_signal_data()
<TimeSeries>
Time:
Time:
TimedeltaIndex(['0 days 00:00:00', '0 days 00:00:02', '0 days 00:00:06'], dtype='timedelta64[ns]', freq=None)
Values:
[10 15 5]
Interpolation:
step
Units:
K
We access the sources’ data by adding its name to the function call:
mc_1.get_signal_data("Thermocouple 1")
<TimeSeries>
Time:
Time:
TimedeltaIndex(['0 days 00:00:00', '0 days 00:00:02', '0 days 00:00:06'], dtype='timedelta64[ns]', freq=None)
Values:
[2 3 1]
Interpolation:
step
Units:
K
Remember, that the returned TimeSeries possesses a plot function that lets you create a plot of the time dependent data:
mc_1.get_signal_data().plot()
<Axes: xlabel='t in s', ylabel='values in K'>
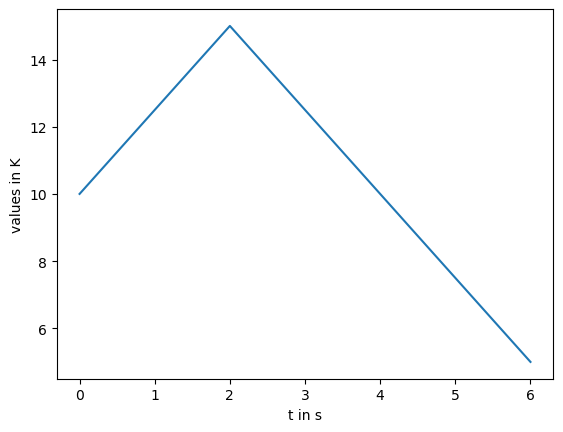
Note that the Signal class returned by the get_signal function offers a plot function too.
So you do not need to fetch the data from the Signal in order to plot it:
mc_1.get_signal("Calibration").plot()
<Axes: xlabel='t in s', ylabel='values in K'>

This concludes this tutorial about the MeasurementChain class.
We have learned different methods to create it, add transformations and measurement data to it.
Additionally, we saw how to define our laboratory equipment using the MeasurementEquipment class and create new measurement chains from it.
An actual welding example that utilizes MeasurementChain can be found here.