6. GenericSeries Tutorial#
6.1. Introduction#
The GenericSeries class describes a potentially multi-dimensional quantity that depends on one or more dimensions.
Some examples are the position of the welding torch that depends on time, or the workpiece temperature field that depends on time and space.
The data of the GenericSeries can either be stored in form of explicit values or as a mathematical expression.
It’s main feature is that you can evaluate the data at any given coordinate of the dimensions it depends on.
This happens either through interpolation if the data is discrete or through direct evaluation of the mathematical expression.
We can use the GenericSeries in our scripts and jupyter notebooks by importing it from the WelDX python package:
from weldx import GenericSeries # isort: off
For this tutorial, we will also need to import the following packages and classes:
import matplotlib.pyplot as plt
import numpy as np
from pint import DimensionalityError
from xarray import DataArray
from weldx import Q_
6.2. Terminology#
Before we can start with the actual tutorial, we need to discuss some terminology. It is essential to understand the differences between the following terms to avoid confusion throughout the course of this tutorial.
Dimension
Each dimension describes a single degree of freedom. We can think of it as a 1d-coordinate axis. Using multiple dimensions will create a multi-dimensional space. A typical example would be the dimensions $x$, $y$, and $z$ that form 3d-space. Another popular dimension is time.
Coordinates
A coordinate is a specific value or label on the 1d-axis of a dimension. We can specify the location of a point in 3d-space by providing its coordinates. For example, we can use $x=1m$, $y=3m$, and $z=0m$. These are coordinates for the dimensions $x$, $y$, and $z$. Dimensions represent degrees of freedom, coordinates are discrete values of a dimension.
Variable
If a mathematical expression is used to describe the GenericSeries, the individual terms of this expression can be divided into two groups.
The first group are variables.
Variables are symbols that don’t get values assigned to them during the creation of a GenericSeries.
They let us evaluate the expression for different coordinates.
Consider the following expression:
$$ 2 \cdot x + 3 $$
Here, $x$ is our variable.
We can evaluate this expression over and over again by providing different values/coordinates for $x$.
For example, if we would use $x=2$, the result is $7$.
With $x=4$ we would get $11$.
An important fact to note is that each variable of a GenericSeries’ expression is a dimension.
But not every dimension of an expression is necessarily represented by a variable.
We will show some code examples later that make this more understandable.
Parameter
The second group of therms in an expression based GenericSeries are parameters.
Parameters are also symbols of an expression, but in contrast to variables, they already get discrete values assigned to them.
Consider the following expression:
$$ a \cdot t + b $$
with:
$$ \begin{matrix} a=&3m/s\ b=&5m \end{matrix} $$
$a$ and $b$ are parameters, because they have values assigned to them.
t is still a variable
Free dimension
Dimensions in an expression can either be represented by a variable or a parameter. To distinguish between both, we will refer to dimensions that are expression variables as “free dimensions”.
6.3. Discrete data#
6.3.1. Construction#
As mentioned in the introduction, the GenericSeries can either describe a dimension dependent quantity by a set of discrete values or a mathematical expression.
We will start this tutorial with discrete values.
Let’s say we want to describe the temperature of a specimen along our welding groove during a single pass welding experiment.
The spatial direction along the groove is the dimension x.
Time is represented by the dimension t.
We have measured the temperature at 4 different points in time and at 6 different positions.
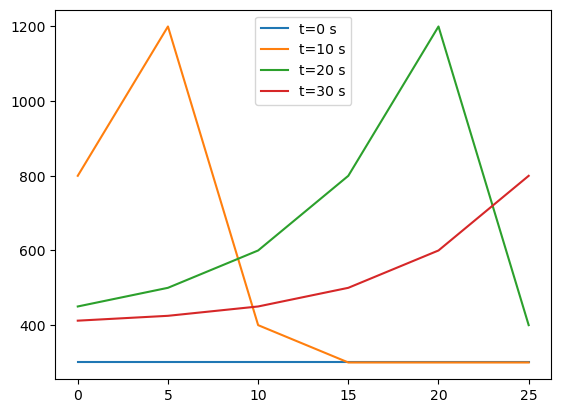
Our data measured in Kelvin is:
t_0 = [300, 300, 300, 300, 300, 300]
t_1 = [800, 1200, 400, 300, 300, 300]
t_2 = [450, 500, 600, 800, 1200, 400]
t_3 = [412, 425, 450, 500, 600, 800]
data = Q_([t_0, t_1, t_2, t_3], "K")
We also know the coordinates of the data in x and t:
coords_t = Q_([0, 10, 20, 30], "s")
coords_x = Q_([0, 5, 10, 15, 20, 25], "cm")
Here is a quick plot of our temperature data:
plt.plot(coords_x.m, np.transpose(data.m), label=[f"t={v}" for v in coords_t])
plt.gca().legend()
<matplotlib.legend.Legend at 0x7f080686a860>
Now we can create our GenericSeries as follows:
gs_discrete = GenericSeries(
obj=data, dims=["t", "x"], coords={"t": coords_t, "x": coords_x}
)
gs_discrete
<GenericSeries>
Values:
[[ 300 300 300 300 300 300]
[ 800 1200 400 300 300 300]
[ 450 500 600 800 1200 400]
[ 412 425 450 500 600 800]]
Dimensions:
('t', 'x')
Coordinates:
t = [ 0 10 20 30] s
x = [ 0 5 10 15 20 25] cm
Units:
K
The first argument is the raw data.
dims expects a list of strings that we can use to give our dimensions names.
With coords we provide the coordinates of our discrete values.
dims and coords are optional.
If you don’t provide dimension names, the GenericSeries will use default names:
GenericSeries(obj=data).dims
('dim_0', 'dim_1')
If you are already familiar with the xarray python package, you might have noticed the similarities between the construction of a GenericSeries and an xarray.DataArray.
In fact, the discrete version of the GenericSeries is based on an xarray.DataArray and they share some interfaces with comparable behavior.
6.4. Evaluation/Interpolation#
Even though the GenericSeries might be based on discrete values, you should think of it as some kind of mathematical function object that can be evaluated at any coordinate along its dimensions.
To do so, we simply use the call operator () on our GenericSeries and specify the coordinates we are interested in.
For example, we might be interested in the temperature at $x=12cm$ and $t=24s$.
The coordinates are passed as keyword arguments where the key is the dimension and the value are the coordinates we are interested in:
gs_discrete(t="0.25mins", x="120mm")
<GenericSeries>
Values:
[[520.]]
Dimensions:
('t', 'x')
Coordinates:
t = [0.25] min
x = [120.] mm
Units:
K
It is not necessary to provide coordinates for all dimensions. A single dimension is already enough:
gs_discrete(t="24s")
<GenericSeries>
Values:
[[434.8 470. 540. 680. 960. 560. ]]
Dimensions:
('t', 'x')
Coordinates:
t = [24] s
x = [ 0 5 10 15 20 25] cm
Units:
K
Of course, we can also evaluate multiple coordinate values for each dimension:
gs_discrete(t=Q_([11, 23], "s"), x=Q_([3, 14, 22], "cm"))
<GenericSeries>
Values:
[[984. 364. 358. ]
[461.94 679. 820. ]]
Dimensions:
('t', 'x')
Coordinates:
t = [11 23] s
x = [ 3 14 22] cm
Units:
K
You may have noticed that we exclusively used coordinate values that do not match the coordinates we initially provided to the GenericSeries.
The actual data values are obtained by interpolation.
By default, the GenericSeries uses linear interpolation.
It can be changed during construction using the interpolation parameter or by assigning a new value using the interpolation setter:
gs_discrete.interpolation = "linear"
In case the provided interpolation coordinates exceed the coordinate range of the series, the corresponding result value will be set to the closest boundary value.
Let’s interpolate the data for $t=15s$ and plot it together with the two closest timesteps:
plt.plot(coords_x.m, np.transpose(gs_discrete(t="15s").data[0].m), label="t=15s")
plt.plot(
coords_x.m,
np.transpose(gs_discrete.data[1:3].m),
label=[f"t={v}s" for v in gs_discrete.data_array.t[1:3].data],
)
plt.gca().legend();
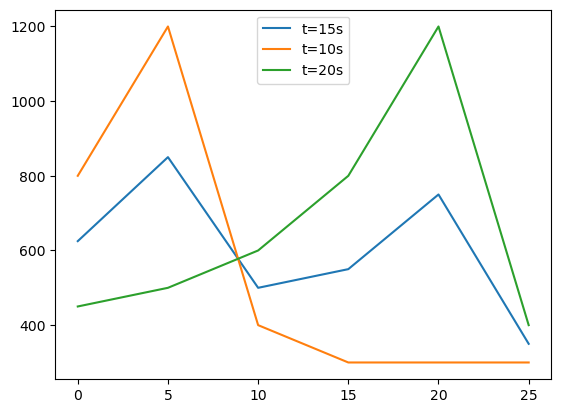
As one might expect the linearly interpolated data is the mean value of both curves since $t=15s$ lies directly in the middle between $t=10s$ and $t=20s$. However, that doesn’t really look like the correct temperature distribution for a single torch moving along the groove. Instead the peak value should translate from left to right. Of cause, with dense data from real measurements, this would be just a minor issue with no practical relevance, but it serves as a nice transition two our next topic.
6.5. Using Expressions#
6.5.1. A simple example#
Another way to define a GenericSeries is using mathematical expressions.
In contrast to the previously shown approach we do not need to generate and store a lot of discrete data.
All we need is a simple formula.
Additionally, we do not get interpolation errors as in the previous section since we can evaluate the expression exactly for any given set of coordinates.
Let’s start with a more or less simple example where we try to depict the data from the previous section as an expression.
Note that we are not thriving for an exact match of the values, since this is only an example of the GenericSeries’s features.
The following equation resembles a single wave that travels towards increasing $x$ values with increasing v $t$:
$$ f\left(x,t\right)=\mathrm{tanh}\left(\frac{x-t}{5}\right) - \mathrm{tanh}\left(x-t-10\right) $$
Like in the previous section, the slope on the right-hand side of the peak is much steeper.
We now translate this equation into an expression string that can be understood by the GenericSeries:
expr = "tanh((x-t)/5) - tanh(x-t-10)"
The syntax is pretty close to python code, except that it is enclosed inside of a string.
Now we could create a MathematicalExpression using this expression string and pass it to the GenericSeries, but it is much easier to simply pass the string directly to the GenericSeries:
TODO Link MathExpr tutorial
gs_expr = GenericSeries(expr)
We have now created a GenericSeries based on an expression.
Wasn’t that hard, right?
Let’s print it and have a look at its representation:
gs_expr
<GenericSeries>
Expression:
-tanh(t/5 - x/5) + tanh(t - x + 10)
Parameters:
NoneFree Dimensions:
x in
t in
Other Dimensions:
[]
Units:
The first item of the output is the expression we entered, but there are also the fields Parameters, Dimensions, and Units.
Our current GenericSeries has no parameters (see terminology at the beginning) since we did not define any so far.
The dimensions x and t were automatically extracted from the provided expression.
The field Units refers to the units our quantity after we evaluated the expression.
As you can see, the field is currently empty and we will soon understand why this is the case.
But first, we will evaluate our equation as we did before with the discrete version, except that we will not use units here.
Again, we will talk about this later.
coords_t = [-5, 5, 15]
coords_x = list(range(25))
result = gs_expr(t=coords_t, x=coords_x)
result
<GenericSeries>
Values:
[[ 1.7615e+00 1.8330e+00 1.8804e+00 ... -4.0798e-05 -2.7348e-05
-1.8332e-05]
[ 2.3841e-01 3.3596e-01 4.6295e-01 ... -2.2234e-03 -1.4918e-03
-1.0004e-03]
[ 4.9452e-03 7.3685e-03 1.0973e-02 ... 1.8804e+00 1.8857e+00
1.7084e+00]]
Dimensions:
('t', 'x')
Coordinates:
t = [-5 5 15]
x = [ 0 1 2 ... 22 23 24]
Units:
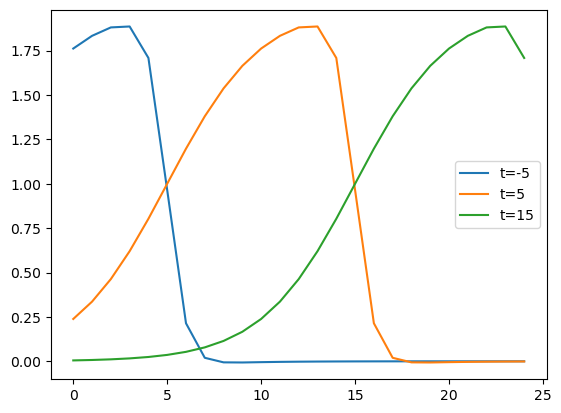
The result is a new GenericSeries with discrete values at the coordinates we provided.
Let’s create a plot from the data:
plt.plot(
result.data_array.x,
np.transpose(result.data.m),
label=[f"t={v}" for v in result.data_array.t.data],
)
plt.gca().legend();
6.5.2. Adding parameters#
While we can already recognize in the previous plot, that it has some similarities with the plot of the discrete data, a look at the y-axis tells us, that the magnitudes do not match.
We will correct this by multiplying with a scaling factor s and adding an offset o.
The new expression is:
expr_param = "s * (tanh((x-t)/5) - tanh(x-t-10)) + o"
So far, there is nothing that distinct s and o from x and t.
They are just another set of symbols in our equation.
We will declare s and o as expression parameters during the construction of our GenericSeries using the parameters argument.
It expects a dictionary, that maps a discrete value to any of our expressions symbols.
Let us now do this for s and o:
gs_expr_param = GenericSeries(
expr_param,
parameters=dict(s=450, o=300),
)
gs_expr_param
<GenericSeries>
Expression:
o + s*(-tanh(t/5 - x/5) + tanh(t - x + 10))
Parameters:
s = 450
o = 300
Free Dimensions:
t in
x in
Other Dimensions:
[]
Units:
As you can see, s and o now appear in the Parameters section together with the values we assigned to them while t and x are still variables.
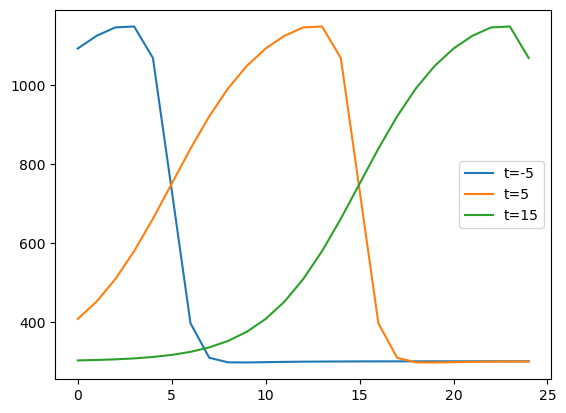
If we plot the new GenericSeries at the same coordinates as before, we can see the effect of our modifications on the y-axis:
result_expr_param = gs_expr_param(t=coords_t, x=coords_x)
plt.plot(
coords_x,
np.transpose(result_expr_param.data.m),
label=[f"t={v}" for v in coords_t],
)
plt.gca().legend();
6.5.3. Adding units#
The final piece we are missing in resembling the discrete data as expression are units. We avoided them so far, so that you don’t get overwhelmed with information and learn things step by step. Adding units is pretty simpel, but you need to watch out that the provided units are actually compatible in context of the expression.
Looking at our equation, $x-t$ already violates this constraint since we can’t subtract a time from a length. It only worked in the previous examples because we didn’t provide any units at all. Note that plain numbers are silently converted to unitless quantities. Furthermore, the hyperbolic tangent requires an angular unit. Python let’s us actually get away with unitless quantities as inputs to the hyperbolic tangent and treats them as radians, but you should not rely on this and always use the correct units.
We can solve these aforementioned issues by simply introducing additional unit conversion parameters.
In our example expression, we introduce the additional parameters a and b to multiply them with with x and t so that the addition is valid and yields an angular unit.
The updated expression now looks like this:
expr_units = "s * (tanh((a*x-b*t)/5) - tanh(a*x-b*t-10)) + o"
We define the values for the parameters as follows:
params_units = dict(s="450K", o="300K", a="rad/cm", b="rad/s")
Note that we added Kelvins as units to s and o.
If we now try to create a new, updated GenericSeries, we will still get an error:
try:
GenericSeries(expr_units, parameters=params_units)
except DimensionalityError:
print("Still got an issue with the dimensions!")
Still got an issue with the dimensions!
The remaining problem here is that the GenericSeries doesn’t know the units of our dimensions x and t.
Because we didn’t specify that, it assumes they are dimensionless.
We can tell the GenericSeries what units those dimensions have by using the units input during initialization.
It requires a simple mapping between the dimension and its unit like in the following example.
gs_units = GenericSeries(expr_units, parameters=params_units, units=dict(x="cm", t="s"))
gs_units
<GenericSeries>
Expression:
o + s*(tanh(a*x/5 - b*t/5) + tanh(-a*x + b*t + 10))
Parameters:
s = 450 K
o = 300 K
a = 1.0 rad / cm
b = 1.0 rad / s
Free Dimensions:
x in cm
t in s
Other Dimensions:
[]
Units:
K
Additional note: Actually, the
GenericSeriesdoesn’t require a unit for a dimension, but a “dimensionality” like length, time, temperature etc. It has no real relevance if you would assign seconds, minutes or hours to a dimension since the unit will be scaled internally
Finally, we are able to construct our GenericSeries that also considers units.
As you can see, all the provided units are now listed in the output above.
Additionally, the output unit of the expression is listed as Kelvin under Units even though it was never explicitly specified.
The GenericSeries is able to determine it on its own from the information it already has.
If we now want to evaluate the expression, we also have to provide the coordinates as quantities with a fitting unit, otherwise we get an error as the following example shows:
coords_t = [-5, 5, 15]
coords_x = [5, 10, 25]
try:
gs_units(t=coords_t, x=coords_x)
except DimensionalityError:
print("You forgot the units!")
You forgot the units!
Adding the correct units fixes the problem:
coords_t = Q_([-5, 5, 15], "h")
coords_x = Q_([5, 10, 25], "km")
gs_units(t=coords_t, x=coords_x)
<GenericSeries>
Values:
[[300. 300. 300.]
[300. 300. 300.]
[300. 300. 300.]]
Dimensions:
('x', 't')
Coordinates:
x = [ 5 10 25] km
t = [-5 5 15] h
Units:
K
In case you wonder, why all the output values are identical, have a look at the input units we used.
If you change them to "s" and "cm" you will see values that are more in line with the previous examples, but they demonstrate that it is not important which units you assign to the dimensions during initialization.
All that matters is the units “dimensionality”.
6.5.4. Parameter dimensions#
When we discussed the terminology, we stated that all variables of an expression based GenericSeries are dimensions, but not all dimensions are variables.
We will now show you a dimension that is not a variable using a short example.
Consider the following linear equation:
expr_linear = "a*t + b"
t is our only variable and represents time.
a and b are parameters.
So far we only used scalar parameters, but nothing hinders us to use arrays as well:
GenericSeries(
expr_linear,
parameters=dict(a=Q_([1, 3, 5], "m/s"), b=Q_([5, 6, 7], "m")),
units=dict(t="s"),
)
<GenericSeries>
Expression:
a*t + b
Parameters:
a = [1 3 5] m / s
b = [5 6 7] m
Free Dimensions:
t in s
Other Dimensions:
['dim_0']
Units:
m
In the output above, we notice that we got an additional dimension we did not define: dim_0.
This happened because we used arrays for our parameters.
An array is another dimension with discrete values.
Since we did not define a dimension name, the GenericSeries assigned one itself, dim_0.
It also assumes that all provided parameters share the same dimensions.
But that doesn’t have to be what we intended.
Maybe we wanted a and b to have different dimensions.
Therefore, we can also assign dimensions to parameters.
This can either be done by providing the parameter as a tuple consisting of value and dimension name or as an xarray.DataArray:
a = (Q_([1, 3, 5], "m/s"), "c")
b = DataArray(Q_([5, 6, 7], "m"), dims=["v"])
gs_array = GenericSeries(
expr_linear,
parameters=dict(a=a, b=b),
units=dict(t="s"),
)
gs_array
<GenericSeries>
Expression:
a*t + b
Parameters:
a = [1 3 5] m / s
b = [5 6 7] m
Free Dimensions:
t in s
Other Dimensions:
['v', 'c']
Units:
m
As you can see, we now have three dimensions, while only one is an actual variable of our expression.
If we evaluate the GenericSeries, the dimensions will be broadcastet and our result will be a new 3 dimensional discrete GenericSeries.
But see for yourself:
gs_array(t=Q_([0, 1], "s"))
<GenericSeries>
Values:
[[[ 5 6 7]
[ 6 7 8]]
[[ 5 6 7]
[ 8 9 10]]
[[ 5 6 7]
[10 11 12]]]
Dimensions:
('c', 't', 'v')
Coordinates:
t = [0 1] s
Units:
m
Parameters can also have more than one dimension:
GenericSeries(
expr_linear,
parameters=dict(
a=Q_([[0, 1], [2, 3]], "m/s"),
b=Q_([1, 2], "m"),
),
units=dict(t="s"),
)
<GenericSeries>
Expression:
a*t + b
Parameters:
a = [[0 1] [2 3]] m / s
b = [1 2] m
Free Dimensions:
t in s
Other Dimensions:
['dim_0', 'dim_1']
Units:
m
Note that if you do not provide custom names for the dimensions, the GenericSeries will just enumerate them as in the example above.
The enumeration is always restarted for each parameter.
So b would actually use the dimension dim_0.
To avoid any problems, always name your dimensions.
If you use a tuple to name the dimensions of a multi-dimensional parameter, the second value has to be a list of names, where the first name refers to the most outer dimension and the last one to the most inner:
GenericSeries(
expr_linear,
parameters=dict(
a=(Q_([[0, 1], [2, 3]], "m/s"), ["c", "v"]), b=(Q_([1, 2], "m"), "v")
),
units=dict(t="s"),
)
<GenericSeries>
Expression:
a*t + b
Parameters:
a = [[0 1] [2 3]] m / s
b = [1 2] m
Free Dimensions:
t in s
Other Dimensions:
['v', 'c']
Units:
m
6.5.5. Partial evaluation#
Like a GenericSeries constructed from discrete values, an expression based GenericSeries can also be evaluated partially.
Here is a short example:
gs_reduced = gs_units(t=Q_([5, 10, 15], "s"))
In this case, we get a new expression-based GenericSeries.
t now becomes a new parameter consisting of the provided values.
As long as we do not provide coordinates for all variables of an expression, evaluating the GenericSeries will transform the corresponding variables into parameters.
Only if all variables get coordinates assigned to them, the resulting GenericSeries will consist of discrete data.
Let’s evaluate the result from the previous evaluation to confirm this:
gs_reduced(x="5cm")
<GenericSeries>
Values:
[[750. 407.2826 316.1876]]
Dimensions:
('x', 't')
Coordinates:
x = [5] cm
Units:
K